Box multiplication
key notes:
⛱️ Box method of multiplication:
- Step 1: Make a table with the place values of the first factor along the top and the place values of the second factor down the left.
- Step 2: Multiply the place values and enter their products in the table.
- Step 3: Sum each row of the table.
- Step 4: Add these row sums. This is the product of the original factors.
Learn with an example
🎯Use the box method to find 50×75.
🎯 Calculate the sums on the right. Add these sums to find 50×75.

🗼 Step 1
To multiply two numbers using the box method, make a table with the place values of the first factor along the top and the place values of the second factor down the left.
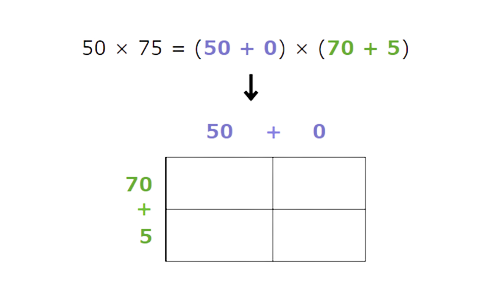
🗼 Step 2
Multiply the place values and enter their products in the table.

- Simplify the table.
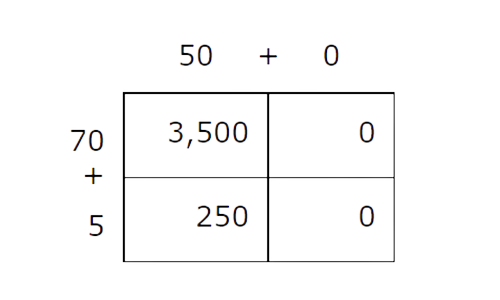
🗼 Step 3
Sum each row of the table.
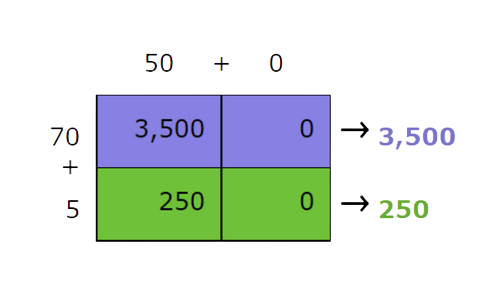
🗼 Step 4
Add these row sums. This is the product of the original factors.
- 3,500+250=3,750
- So, 50×75=3,750.
🎯Use the box method to find 49×50.
🎯 Calculate the sums on the right. Add these sums to find 49×50.
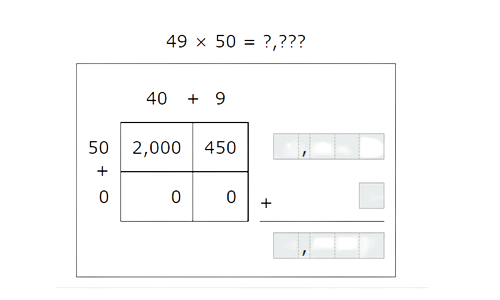
🗼 Step 1
To multiply two numbers using the box method, make a table with the place values of the first factor along the top and the place values of the second factor down the left.
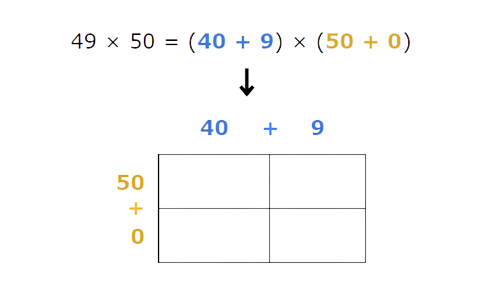
🗼 Step 2
Multiply the place values and enter their products in the table.
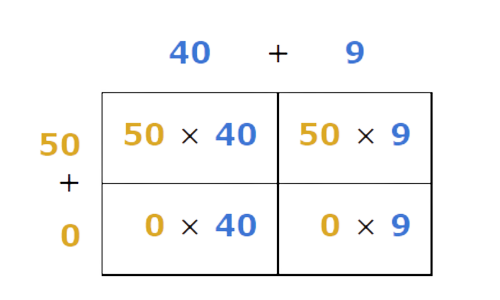
- Simplify the table.
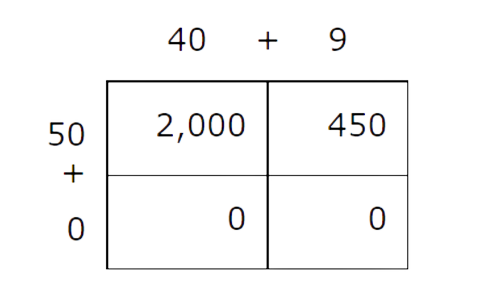
🗼 Step 3
- Sum each row of the table.
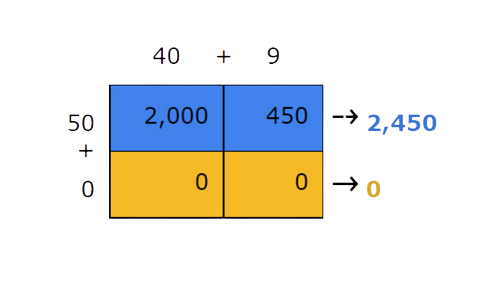
🗼 Step 4
Add these row sums. This is the product of the original factors.
- 2,450+0=2,450
- So, 49×50=2,450
🎯 Use the box method to find 22×82.
🎯 Calculate the sums on the right. Add these sums to find 22×82.
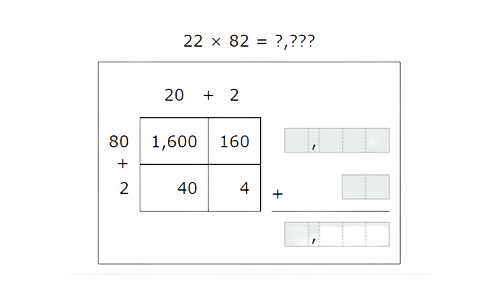
🗼 Step 1
To multiply two numbers using the box method, make a table with the place values of the first factor along the top and the place values of the second factor down the left.
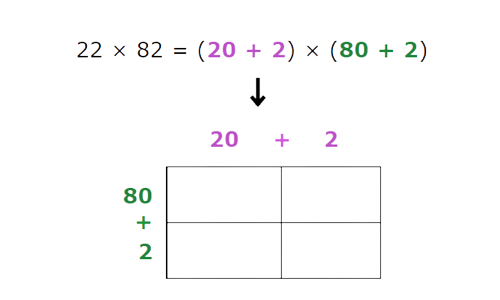
🗼 Step 2
Multiply the place values and enter their products in the table.
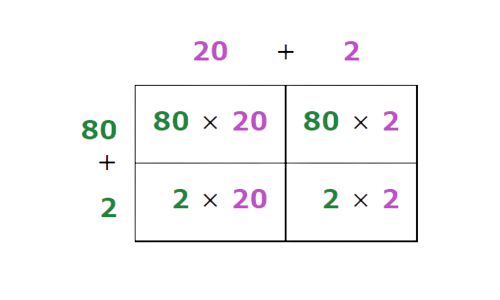
- Simplify the table.
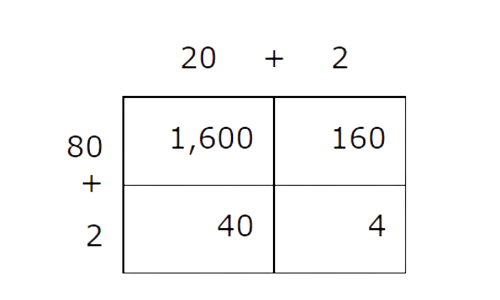
🗼 Step 3
Sum each row of the table.
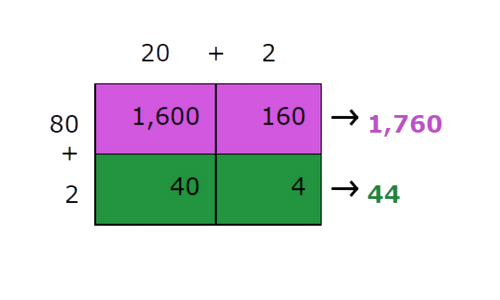
🗼 Step 4
Add these row sums. This is the product of the original factors.]
- 1,760+44=1,804
- So, 22×82=1,804.
Let’s practice!🖊️

