Lattice multiplication
key notes:
Introduction to Lattice Multiplication:
- Definition: Lattice multiplication is a method for multiplying large numbers using a grid or lattice.
- Purpose: It helps break down complex multiplication problems into smaller, more manageable parts.
Setting Up the Lattice:
- Create the Grid: Draw a grid with as many rows and columns as there are digits in the numbers being multiplied. For example, if multiplying a 2-digit number by another 2-digit number, draw a 2×2 grid.
- Label the Grid: Write one of the numbers along the top of the grid (one digit per column) and the other number along the side of the grid (one digit per row).
Filling in the Lattice:
- Multiply Each Pair: For each cell in the grid, multiply the digit at the top of the column by the digit on the side of the row.
- Write the Product: Write the product in each cell of the grid. The product is split into two parts: the tens digit and the units digit. Write the tens digit in the upper triangle of the cell and the units digit in the lower triangle.
Learn with an example
🎯Use the lattice method to find 41×42.
🎯 Calculate the sum of each diagonal. Your answers for the sums will fill in the answer for the product.
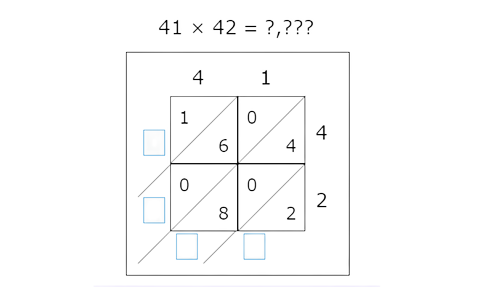
📗 Step 1
To multiply two numbers using the lattice method, make a table with the digits of the first factor along the top and the digits of the second factor down the right. Draw diagonal lines from the top right to the bottom left of each box in the table.
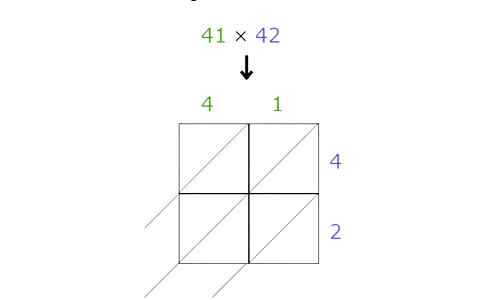
📗 Step 2
Multiply the digits and enter their products in the table. The diagonal in each box separates the digits in each product. For 1-digit products, put a 0 to the left of the diagonal.
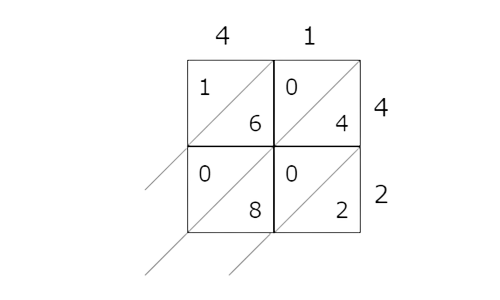
📗 Step 3
Sum each diagonal starting from the bottom right. Make sure to carry for sums greater than 10. Here are the first two diagonals shown:
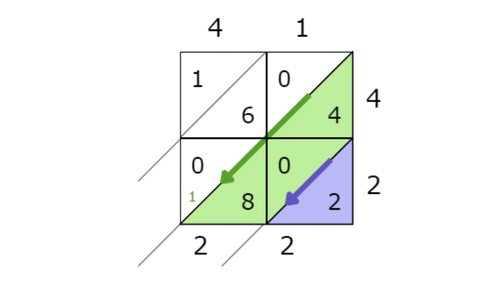
- Notice the carried digit, 1. Find the sums for the rest of the diagonals.
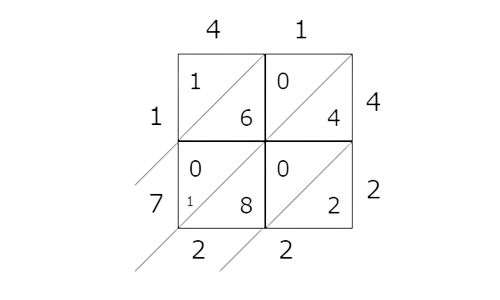
📗 Step 4
Rewrite these sums as a string of digits in order from top to bottom, then left to right. This is the product of the original factors.
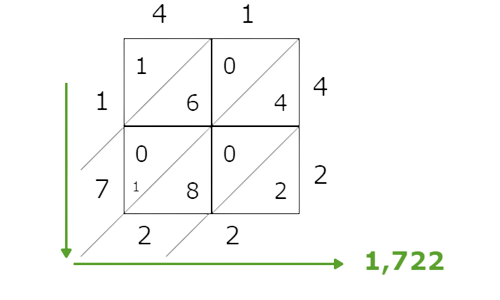
- So, 41×42=1,722.
🎯 Use the lattice method to find 58×66.
🎯 Calculate the sum of each diagonal. Your answers for the sums will fill in the answer for the product.
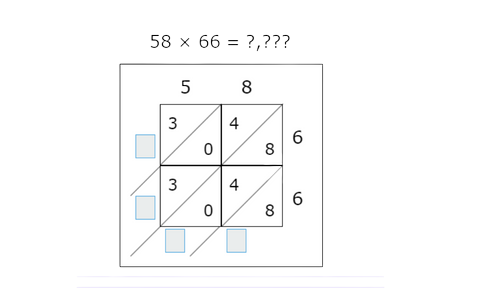
📗 Step 1
To multiply two numbers using the lattice method, make a table with the digits of the first factor along the top and the digits of the second factor down the right. Draw diagonal lines from the top right to bottom left of each box in the table.
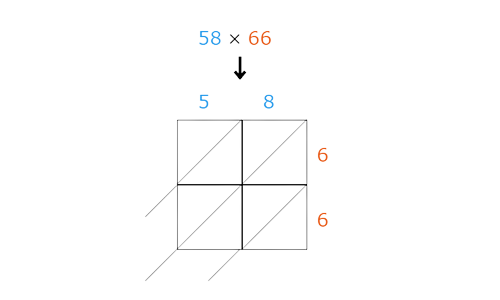
📗 Step 2
Multiply the digits and enter their products in the table. The diagonal in each box separates the digits in each product. For 1-digit products, put a 0 to the left of the diagonal.
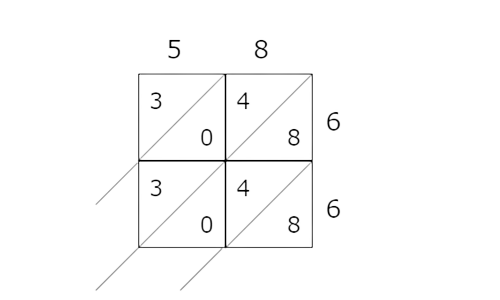
📗 Step 3
Sum each diagonal starting from the bottom right. Make sure to carry for sums greater than 10. Here are the first two diagonals shown:
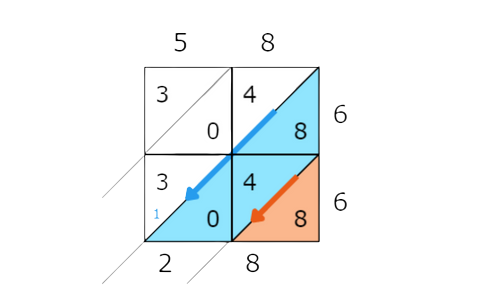
- Notice the carried digit, 1. Find the sums for the rest of the diagonals.
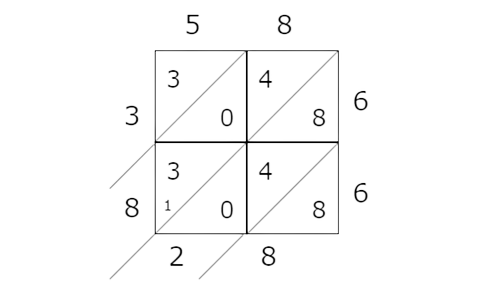
📗 Step 4
Rewrite these sums as a string of digits in order from top to bottom, then left to right. This is the product of the original factors.
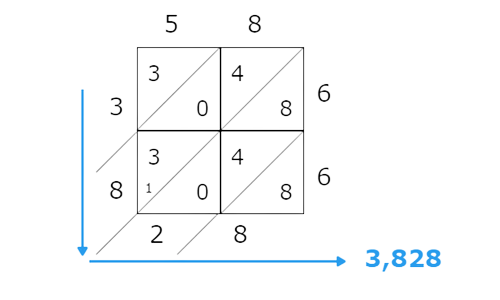
- So, 58×66=3,828.
🎯 Use the lattice method to find 77×48.
🎯 Calculate the sum of each diagonal. Your answers for the sums will fill in the answer for the product.
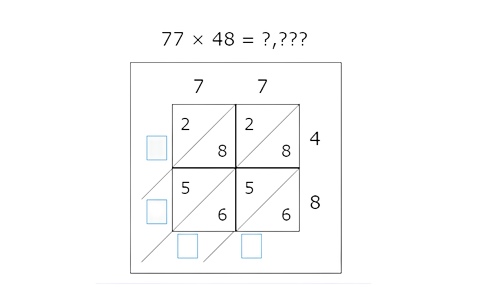
📗 Step 1
To multiply two numbers using the lattice method, make a table with the digits of the first factor along the top and the digits of the second factor down the right. Draw diagonal lines from the top right to the bottom left of each box in the table.
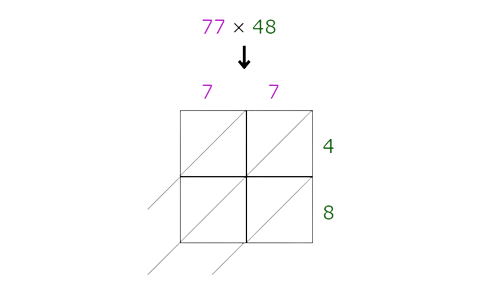
📗 Step 2
Multiply the digits and enter their products in the table. The diagonal in each box separates the digits in each product. For 1-digit products, put a 0 to the left of the diagonal.
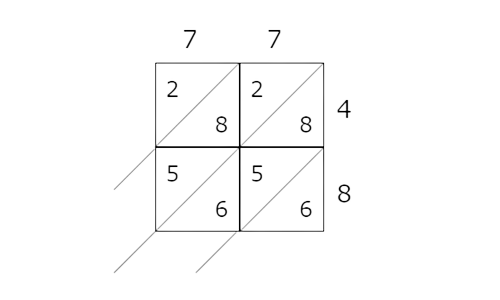
📗 Step 3
Sum each diagonal starting from the bottom right. Make sure to carry for sums greater than 10. Here are the first two diagonals shown:
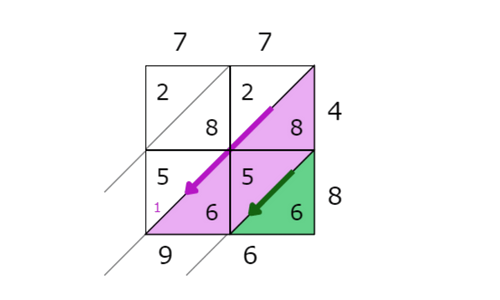
- Notice the carried digit, 1. Find the sums for the rest of the diagonals.
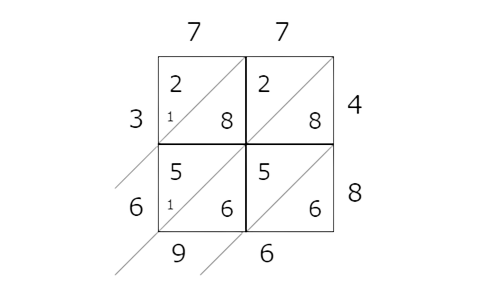
📗 Step 4
Rewrite these sums as a string of digits in order from top to bottom, then left to right. This is the product of the original factors.

- So, 77×48=3,696.
Let’s practice!🖊️

