Divide larger numbers

key notes:

Dividing by 1-digit numbers:

🥏 Dividing a 2-digit number by a 1-digit number

You can use long division to divide numbers. Follow the steps below to divide a 2-digit number by a 1-digit number. Try it with 92÷4.

Write the problem using a long division symbol.

The division problem ninety-two divided by four.

To divide, start with the digit in the tens place. Find how many times 4 goes into 9.

The division problem ninety-two divided by four, with the first step shown. There is a two above the nine. Below the nine, the number eight is subtracted to get one left over.
  • It goes in 2 times.
  • Write the 2 above the 9.
  • Multiply 4×2=8. Write the 8 below the 9.
  • Subtract 9–8=1.
  • There is 1 left over.

Next, bring the 2 down from the ones place to make the number 12. Find how many times 4 goes into 12.

The division problem ninety-two divided by four, with the second step shown. The number twenty-three is shown above ninety-two. Below the nine, the number eight is subtracted to get one left over. An arrow shows bringing the two from ninety-two down next to the leftover one, to make the number twelve. Under the twelve is another twelve subtracted to get a remainder of zero.
  • It goes in 3 times.
  • Write the 3 above the 2.
  • Multiply 4×3=12. Write the 12 below the 12.
  • Subtract 12–12=0.
  • There are 0 left over.

So, 92÷4=23!

🥏 Dividing a 3-digit number by a 1-digit number

You can use long division to divide larger numbers, too. Follow the steps below to divide a 3-digit number by a 1-digit number. Try it with 769÷3.Write the problem using a long division symbol.

The division problem seven hundred sixty-nine divided by three.

To divide, start with the digit in the hundreds place. Find how many times 3 goes into 7.

The division problem seven hundred sixty-nine divided by three, with the first step shown. There is a two above the seven. Below the seven, the number six is subtracted to get one left over.

It goes in 2 times.Write the 2 above the 7.Multiply 3×2=6. Write the 6 below the 7.Subtract 7–6=1.There is 1 left over.Next, bring the 6 down from the tens place to make the number 16. Find how many times 3 goes into 16.

The division problem seven hundred sixty-nine divided by three, with the second step shown. The numbers two and five are shown above seven and six. Below the seven, the number six is subtracted to get one left over. An arrow shows bringing the six down next to the leftover one, to make the number sixteen. Under the sixteen is a fifteen subtracted to get one left over.

It goes in 5 times.Write the 5 above the 6.Multiply 3×5=15. Write the 15 below the 16.Subtract 16–15=1.There is 1 left over.Then, bring down the 9 from the ones place to make the number 19. How many times does 3 go into 19?

The division problem seven hundred sixty-nine divided by three, with the third step shown. The number two hundred fifty-six is shown above seven hundred sixty-nine. Below the seven, the number six is subtracted to get one left over. An arrow shows bringing the six down next to the leftover one, to make the number sixteen. Under the sixteen is a fifteen subtracted to get one left over. Another arrow shows bringing the number nine down next to the one left over to make nineteen. Below the nineteen, the number eighteen is subtracted to get a remainder of 1.

It goes in 6 times.Write the 6 above the 9.Multiply 3×6=18. Write the 18 below the 19.Subtract 19–18=1.There is 1 left over.We have 1 left over. There are no more digits to divide, so 1 is a remainder. That means 3 doesn’t go into 769 evenly. We write the remainder as R1.

All of the steps of the division problem seven hundred sixty-nine divided by three written out. The final answer, two hundred fifty-six remainder one, is written on top.

So, 769÷3=256 R1!

🥏Dividing a 4-digit number by a 1-digit number

You can follow the same steps to divide a 4-digit number by a 1-digit number. Try it with 3,042÷6. Write the problem.

The division problem three thousand forty-two divided by six.

Start with the digit in the thousands place. But, 6 does not go into 3. So, we look at the thousands and the hundreds together. They make the number 30. Find how many times 6 goes into 30.

The division problem three thousand forty-two divided by six, with the first step shown. There is a five above the zero. Below the three and zero, the number thirty is subtracted to get zero left over.

It goes in 5 times.Write the 5 above the 0.Multiply 6×5=30.Subtract 30–30=0.There are 0 left over.Next, bring the 4 down from the tens place to make the number 4. How many times does 6 go into 4?

The division problem three thousand forty-two divided by six, with the second step shown. The digits five and zero are shown above the zero and four of the dividend. Below the three and zero of the dividend, the number thirty is subtracted to get zero left over. An arrow shows bringing the four down next to the leftover zero. Below the four, zero is subtracted to get four left over.

It goes in 0 times. Write the 0 above the 4. Multiply 6×0=0. Subtract 4–0=4. There are 4 left over. Then, bring down the 2 from the one place to make the number 42. How many times does 6 go into 42?

The division problem three thousand forty-two divided by six, with the third step shown. The digits five, zero, and seven are shown above the zero, four, and two of the dividend. Below the three and zero of the dividend, the number thirty is subtracted to get zero left over. An arrow shows bringing the four down next to the leftover zero. Below the four, zero is subtracted to get four left over. Another arrow shows bringing down the two in the dividend to go next to the leftover four, to make the number forty-two. Below the forty-two, forty-two is subtracted for a remainder of zero.

It goes in 7 times. Write the 7 above the 2. Multiply 6×7=42. Subtract 42–42=0. There are 0 left over. We have 0 left over. That means there is no remainder. So, 3,042÷6=507!

Learn with an example

Divide:

581 ÷ 2 =  _____ R ______

Rewrite the problem:

The first digit is greater than 2. Start with the first digit. Divide the hundreds.

Bring down the tens. Divide the tens.

Bring down the ones. Divide the ones.

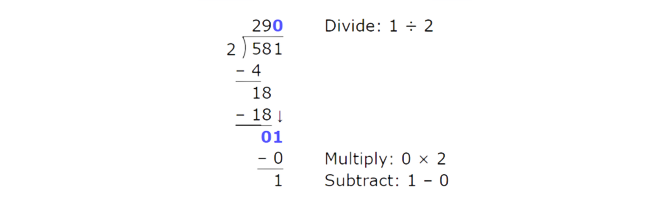
The remainder is 1. Write the answer:

581 ÷ 2 = 290 R1

Divide:

52 ÷ 5 =  ______ R _____

Rewrite the problem:

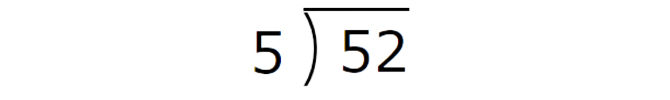
The first digit is equal to 5. Start with the first digit. Divide the tens.

Bring down the ones. Divide the ones.

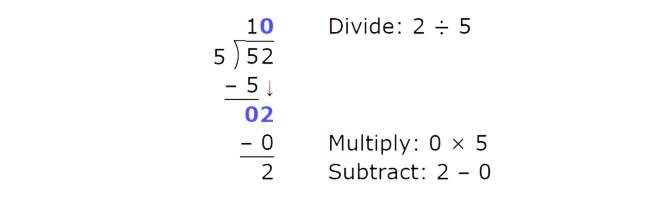
The remainder is 2. Write the answer:

52 ÷ 5 = 10 R2

Divide:

91 ÷ 9 = ____  R _____

Rewrite the problem:

The first digit is equal to 9. Start with the first digit. Divide the tens.

Bring down the ones. Divide the ones.

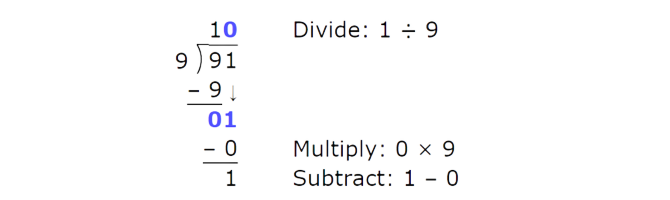
91 ÷ 9 = 10 R1

Let’s practice!