Add, subtract, multiply, and divide

key notes :

1. Addition

  • Definition: Combining two or more numbers to get a total.
  • Symbols: The plus sign (+) is used for addition.
  • Example: 4+3=7
  • Properties:
    • Commutative Property: Order does not matter (e.g., 3+5=5+3).
    • Associative Property: Grouping does not matter (e.g., (2+3)+4=2+(3+4)
    • Identity Property: Adding zero does not change the number (e.g., 7+0=7).

2. Subtraction

  • Definition: Finding the difference between two numbers by taking one number away from another.
  • Symbols: The minus sign (−) is used for subtraction.
  • Example: 9−5=4
  • Properties:
    • Not Commutative: Order matters (e.g., 5−3≠3−5).
    • Identity Property: Subtracting zero does not change the number (e.g., 6−0=6).

3. Multiplication

  • Definition: Adding a number to itself a certain number of times.
  • Symbols: The multiplication sign (×) is used for multiplication.
  • Example: 4×3=12 (This means 4+4+4=12)
  • Properties:
    • Commutative Property: Order does not matter (e.g., 2×3=3×2).
    • Associative Property: Grouping does not matter (e.g., (2×3)×4=2×(3×4)).
    • Identity Property: Multiplying by one does not change the number (e.g., 5×1=5).
    • Zero Property: Multiplying by zero results in zero (e.g., 8×0=0).

4. Division

  • Definition: Splitting a number into equal parts or groups.
  • Symbols: The division sign (÷) is used for division.
  • Example: 12÷4=3 (This means 12 is split into 4 equal groups of 3).
  • Properties:
    • Not Commutative: Order matters (e.g., 12 ÷ 4 ≠ 4 ÷ 12 ).
    • Identity Property: Dividing by one does not change the number (e.g., 7÷1=7).
    • Zero Property: Dividing zero by any number results in zero (e.g., 0÷5=0), but division by zero is undefined.

Learn with an example

Add: 34396 and 58124.

Solution:

Step I: Add the ones. 6 + 4 = 10 ones = 1 ten and 0 one. Write 0 in one’s column and carry 1 to the tens column.

Step II: Add the tens. 9 + 2 + 1 (carry over) = 12 tens. 12 tens = 1 hundreds and 2 tens. Write 2 in the tens column and carry 1 to the hundreds column.

Step III: Add the hundreds. 3 + 1 + 1 (carry over) = 5 hundreds. Write 5 in the hundreds column.

Step IV: Add the thousands column. 4 + 8 = 12 thousands. 12 thousands = 1 ten thousand and 2 thousands. Write 2 in the thousands column.

Step V: Add the ten thousand column. 3 + 5 + 1 (carry over) = 9 ten thousands. Write 9 in ten thousand columns.

Adding 5-digit Numbers with Regrouping
Hence, 34396 + 58124 = 92520

1 11
34396
58124
92,520

📗Multiply.

95 x 7=___________

  • Multiply the ones. Remember to carry over.
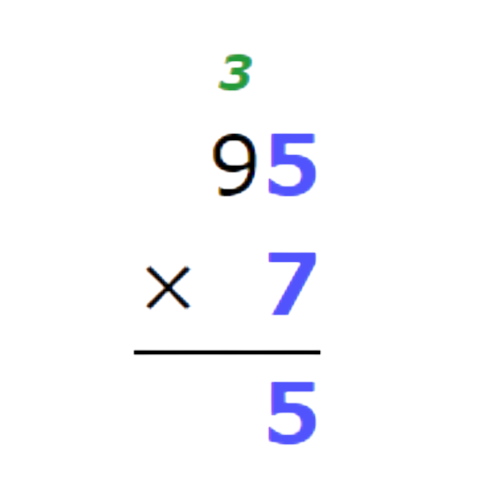
  • Multiply the tens. Multiply 9 times 7, then add 3.
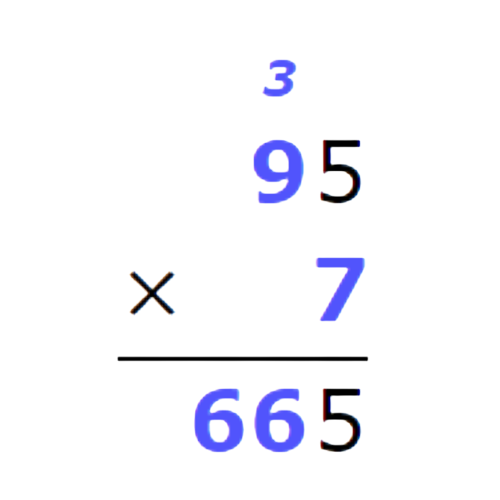
  • The product is 665.

📗 Multiply.

314 x 2=_____

  • Multiply the ones.
  • 314 x 2 =8
  • Multiply the tens.
  • 314 x 2 = 28
  • Multiply the hundreds.
  • 314 x 2 = 628
  • The product is 628.

📗 Subtract.

798-721=____

  • Subtract the ones. Subtract 8–1.
  • 798-721=1
  • Subtract the tens. Subtract 9–2.
  • 798-721=77
  • Subtract the hundreds. Subtract 7–7.
  • 798-721=077
  • The difference is 77.

🥏 Dividing a 3-digit number by a 1-digit number

You can use long division to divide larger numbers, too. Follow the steps below to divide a 3-digit number by a 1-digit number. Try it with 769÷3.

Write the problem using a long division symbol.

The division problem seven hundred sixty-nine divided by three.

To divide, start with the digit in the hundreds place. Find how many times 3 goes into 7.

The division problem seven hundred sixty-nine divided by three, with the first step shown. There is a two above the seven. Below the seven, the number six is subtracted to get one left over.

It goes in 2 times. Write the 2 above the 7. Multiply 3×2=6. Write the 6 below the 7. Subtract 7–6=1. There is 1 left over. Next, bring the 6 down from the tens place to make the number 16. Find how many times 3 goes into 16.

The division problem seven hundred sixty-nine divided by three, with the second step shown. The numbers two and five are shown above seven and six. Below the seven, the number six is subtracted to get one left over. An arrow shows bringing the six down next to the leftover one, to make the number sixteen. Under the sixteen is a fifteen subtracted to get one left over.

It goes in 5 times. Write the 5 above the 6. Multiply 3×5=15. Write the 15 below the 16. Subtract 16–15=1. There is 1 left over. Then, bring down the 9 from the ones place to make the number 19. How many times does 3 go into 19?

The division problem seven hundred sixty-nine divided by three, with the third step shown. The number two hundred fifty-six is shown above seven hundred sixty-nine. Below the seven, the number six is subtracted to get one left over. An arrow shows bringing the six down next to the leftover one, to make the number sixteen. Under the sixteen is a fifteen subtracted to get one left over. Another arrow shows bringing the number nine down next to the one left over to make nineteen. Below the nineteen, the number eighteen is subtracted to get a remainder of 1.

It goes in 6 times.Write the 6 above the 9.Multiply 3×6=18. Write the 18 below the 19.Subtract 19–18=1.There is 1 left over.We have 1 left over. There are no more digits to divide, so 1 is a remainder. That means 3 doesn’t go into 769 evenly. We write the remainder as R1.

All of the steps of the division problem seven hundred sixty-nine divided by three written out. The final answer, two hundred fifty-six remainder one, is written on top.

So, 769÷3=256 R1!

Let’s practice!🖊️